Conditional independence is a crucial building block of probabilistic graphical models (e.g., Bayesian networks). Thus, having a sound understanding of this concept is a must before diving into the topic of Bayesian networks.
This post provides an intuitive introduction to the concept, and then uses a variety of examples to solidify the concept.
At a glance:
- Independence: Two variables don’t affect each other.
- Dependence: Knowing one changes what we believe about the other.
- Conditional independence: Two variables appear related, but once a third variable is known, their relationship disappears.
Dependence and Independence
Two random variables A and B are considered as independent if one does not influence the other. In other terms, the knowledge about one does not change our belief about the other.
Let’s take a student example.
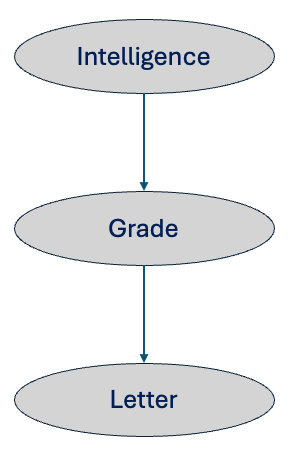
- A student’s intelligence influences their grade.
- A higher grade increases their chance of getting a recommendation letter.
As a quick contrast, imagine linking “student intelligence” to something random, like the number of bicycles in the city 🚲. Clearly, these two are unrelated — knowing one tells us nothing about the other. That’s independence in action.
If two variables are independent, learning one doesn’t change what we know about the other.
\[P(A,B) = P(A) * P(B) \]
We know from Bayes’ theorem that \(P(A,B)=P(A)P(B|A)\), where \(P(B|A)\) represents the probability of B given A. These two expressions can only be equal to each other if \(P(B|A) = P(B)\)
The independence between two random variables is expressed using the following mathematical notations.
\[\begin{multline} \shoveleft P(A,B) = P(A) * P(B) \\ \shoveleft P(A) = P(A|B) \\ \shoveleft P(B) = P(B|A) \end{multline}\]
The joint probability distribution below shows one example of two independent random variables A and B with probabilities \(P(A=1)=.5\) and \(P(B=1)=.5\).
Each entry in the table satisfies the condition of \(P(A,B)=P(A)P(B)\). For example, \(P(A=1,B=1) = .5 * .5 = .25\)
| A | B | P(A,B) |
|---|---|---|
| 0 | 0 | 0.25 |
| 0 | 1 | 0.25 |
| 1 | 0 | 0.25 |
| 1 | 1 | 0.25 |
Conditional Independence
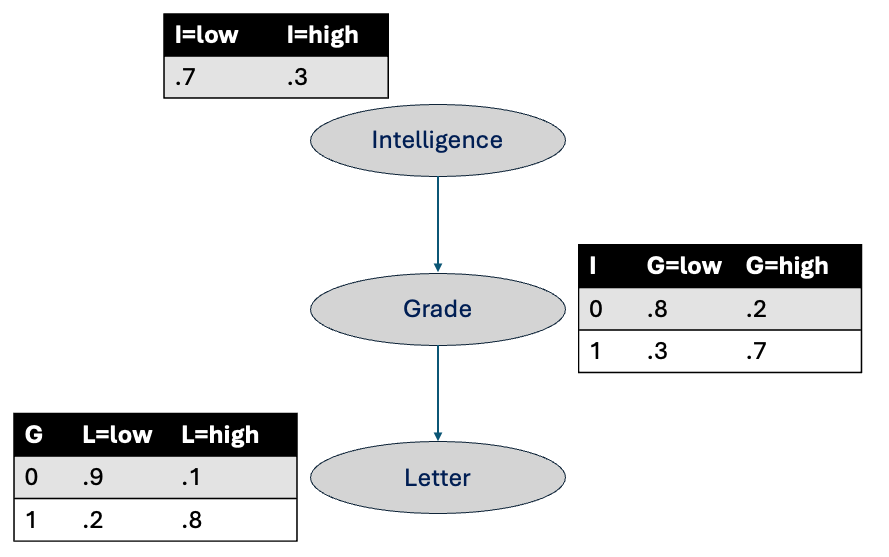
I will start with the following example representing our belief about a highly intelligent student likely to get a higher grade, which increases his chances of getting a recommendation letter from the class’s professor.
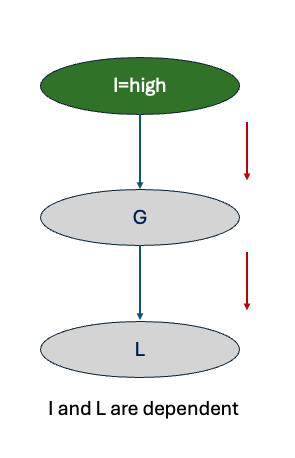
We get to know that student X is highly intelligent. This information immediately tells us that the student is likely to achieve a higher grade and that increases his chances of getting a recommendation letter.
We will now compute \(P(L=1|I=1)\). For that, we need \(P(L=1,I=1)\), which can be computed using the chain rule.
Applying Bayes rule \[\begin{multline} \shoveleft P(L=1|I=1) = \frac{P(L=1,I=1)}{P(I=1)} \end{multline}\]
Here’s how intelligence affects the probability of getting a letter:
| I (Intelligence) | G=1 (High Grade) | P(L=1 | G) |
|---|---|---|---|
| 1 (High) | 0.7 | 0.8 | 0.56 |
| 1 (High) | 0.3 | 0.1 | 0.03 |
Total: 0.59
Similarily, we can compute \(P(L=1|I=0)\) which comes as \(.24\). As we can see, the probability of getting a high grade decreases, and it reduces the chances of getting a recommendation letter.
- For high intelligent student P(L=1)= .59
- For low intelligent student P(L=0)=.24
The probability of getting a recommendation letter increases corresponding to the student’s intelligence.
These example illustrates how influence travels from intelligence to grade and then grade to letter. It clearly shows that Intelligence and letter are dependent. In other terms, if we have information only about a student’s intelligence, then it updates our belief about the chances of that student getting a letter.
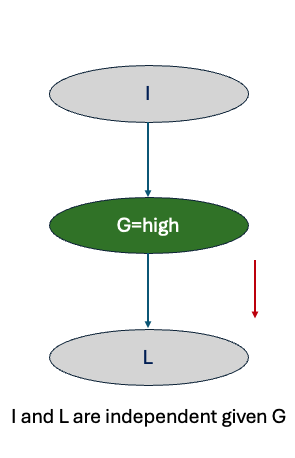
What if we directly get to know that a student has achieved a high grade?
We can immediately tell the student is likely to get a recommendation letter. In this case, knowing about the student’s intelligence will not add anything because the letter depends on the grade.
✨ Key takeaway: Intelligence and letter only look dependent until grade is revealed. Once the grade is known, the letter ignores intelligence.
The mathematical notation for conditional independence is as follows.
Summary: Independence means no influence. Dependence means knowledge updates our beliefs. Conditional independence means the relationship disappears once we know a “mediating” variable. In Bayesian networks, this is the key property that makes them powerful and efficient.